グループテスト

グループテストは，多数の対象から少数の特定のものを効率的に識別するための数理的手法です．

グループテストは，もともと血液検査を通じて梅毒の陽性者を効率的に発見するために提案されましたが，現在では欠陥品の検出，ネットワークセキュリティ，DNAスクリーニングやPCR検査など，さまざまな分野で応用されています．特に感染症検査では，多数の検体から陽性者を早期に発見する手法として多く用いられ，その効率性が高く評価されています．

グループテストでは，検査対象（以下「検体」と呼ぶ）を複数まとめた「プール」と呼ばれるグループ単位でテストを行い，総検査回数を減らしつつ，目的物（以下「陽性検体」と呼ぶ）を特定することを目指します．

検体を1つずつ個別にテストする場合，検体の数が増えると検査回数も線形的に増加します．しかし，グループテストでは特定のグループ内に少なくとも1つの陽性検体が含まれているかを確認することで，複数の検体を同時に調べることが可能です．この方法は，陽性検体の割合が低い場合に特に有効です．例えば，1万個の検体の中にわずか数個の陽性検体が存在する場合，1つずつ検査する代わりに，数十個ずつまとめてテストすることで，効率的に陽性検体を特定できます．このアプローチにより，検査回数が大幅に削減され，検査コストや時間の節約につながります．

小さい例として，7人（1番〜7番）の検体から高々1つの陽性検体を検出することを考えます． そのために，以下の3つのプールを考えます：

• プール $A = \{1, 4, 5, 7\}$
• プール $B = \{2, 4, 6, 7\}$
• プール $C = \{3, 5, 6, 7\}$

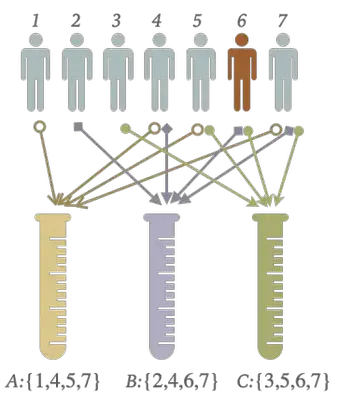
ここで，1つの検体を分けて複数のプールに含めることがあります．

このようなグループテストでは，A，B，C に対して3回のテストがあれば十分です．

たとえば，B と C のテストが陽性で，A が陰性である場合を考えてみましょう．まず，A が陰性なので，A に含まれる1, 4, 5, 7 が陰性であることがわかります．そして，B が陽性となった原因は 2 または 6 にしかありえません．同様に，C が陽性となった原因は 3 または 6 にしかありえません．もし陽性検体が1つだけなら，検体 6 が陽性であるのが唯一の可能性となります．

上の例のように，グループテストはデザインとデコーディングの2つの段階に分けられます．

デザインの段階では，どの検体をどのプールに配置するかを決定します．前の例のようなプールの集合 {A, B, C} はプーリングデザイン（pooling design）と呼ばれます．プーリングデザインの生成方法はさらに適応型と非適応型の2つに分けられます． 適応型テストでは，前の各テスト結果に基づいてプールが逐次的に生成されます．一方，非適応型テストは，全てのプール（つまり，プーリングデザイン）を事前に決定する方法であるため，各テストが並列に実行可能です． 上記の例は，非適応型テストの一例です． 非適応型テストのための効率的なプーリングデザインの生成は，組合せデザイン理論に深く関係しており，グループテストの理論研究において非常に重要です．

デコーディングの段階では，実施されたテストの結果から，どの検体が陽性であるかを推定します．デコーディングの方法として，上記の例のようにシンプルな（排除法のような）推定アルゴリズムもあれば，ベイジアンネットワークに基づいた確率推定アルゴリズムも応用されています．

また，現実の応用においては，テストに誤りがある場合，つまり偽陰性や偽陽性を考慮する必要があります．さらに，テストにプールサイズの制限などを考慮しなければならない場合もあります．

本研究室では，グループテスト問題と上記のような各種のバリエーションについて，デザインの数理的研究とデコーディングに関するアルゴリズムの研究の両方を取り組んでいます．