組合せデザイン
組合せデザイン理論は,建築や芸術の「デザイン」とは異なり,離散数学における「均整性」(対称性やバランス性)を持つ組合せ構造を研究する分野です. 要素の集合を特定の条件を満たしながら「上手く」配置することで,統計的実験計画法,符号理論,暗号理論など,さまざまな応用分野で重要な役割を果たします.
例えば,3人で対戦するゲームを7人で遊ぶことを考えましょう.各プレイヤーが他の全員と1度ずつ対戦する公平な対戦表を作成しようとします.ここで,プレヤー7人を $0$ から $6$ までの数字で表します.以下の対戦表を見てみましょう.ここで,$\{a,b,c\}$ は3人のプレヤー $a$, $b$, $c$ が1回対戦することを意味します.
| ラウンド | 参加プレイヤー |
|---|---|
| 1 | $\{0, 1, 3\}$ |
| 2 | $\{1, 2, 4\}$ |
| 3 | $\{2, 3, 5\}$ |
| 4 | $\{3, 4, 6\}$ |
| 5 | $\{4, 5, 0\}$ |
| 6 | $\{5, 6, 1\}$ |
| 7 | $\{6, 0, 2\}$ |
この対戦表は,グラフと呼ばれる離散数学構造で表すことができます.以下の図では,点を結ぶ辺は2人の対戦関係を表し,1つの三角形が1回の対戦を表しています.各辺が唯一の三角形に含まれていることから,どの2人も1回ずつ対戦することがわかります.この三角形に分解する配置は Steiner Triple System として知られる「組合せデザイン」の一種です.
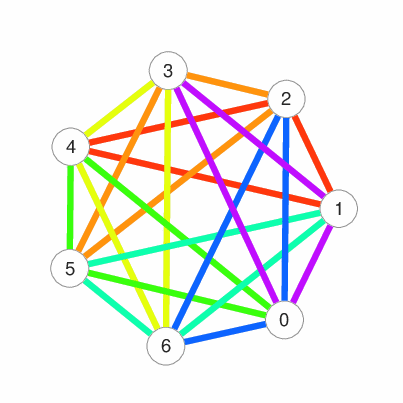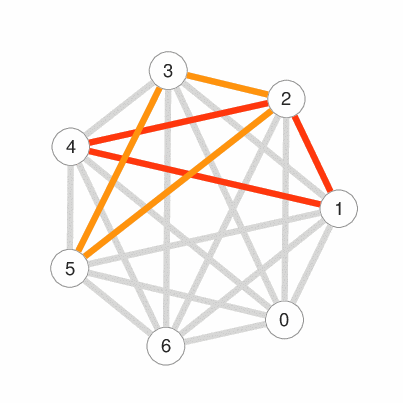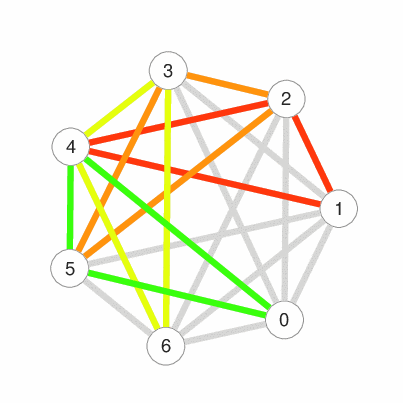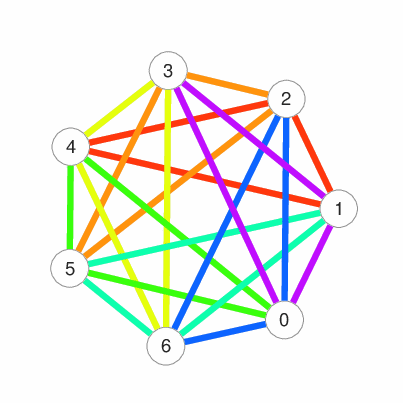
統計学においては,実験によってデータを収集する前に実験を「デザイン」することによって,データ解析の精度を高めることがあります.また,情報通信分野では,送信する情報の符号化を巧妙に「デザイン」することで,送信過程で発生する誤りを検出・訂正することが可能となります.さらに,秘密情報の分散管理方式を「デザイン」することで,漏洩のリスクから秘密情報を最大限に守ることができます.これらの様々な分野の「デザイン」は「組合せデザイン」と深く関係しており,古くから研究されてきました.近年では,組合せデザイン理論とソフトウェア工学,大規模分散ストレージシステムなどの情報工学分野との学際的研究も盛んに行われています.